人生物信息学中的机器学习
- SVM, Artificial neural networks, Hidden Markov Model…


中国早期机器学习在生物学中的应用
- 清华大学孙之荣教授:
- 1997年,将人工神经网络引入生物信息学领域;
- 1999年,利用支持向量机预测可变剪接位点;
- 2001年,构建蛋白质细胞亚定位预测工具SubLoc,以及蛋白质二级结构预测算法。
生物医学中的六种数据类型
- 序列数据:DNA、RNA、蛋白质序列
- 结构数据:NMR、X-ray、Cryo-EM/Cryo-ET
- 遗传/进化距离数据
- 谱数据:基因芯片、蛋白质-蛋白质相互作用
- 影像数据: 图像、视频(CT、MRI、超声)
- 文本数据:科学文献、电子病历
- 混合数据:二代测序数据(序列、谱)
模型评估与选择
- 样本/检验数据:阳性数据 (P),阴性数据 (N)
- 阳性数据 (P):真实的,被实验所证实的数据
- 阴性数据 (N):被实验所证明为无功能的数据
- 对于预测结果的评估,定义:
- 真阳性 (TP): 阳性数据中被预测为阳性的数据
- 假阳性 (FP): 阴性数据中被预测为阳性的数据
- 真阴性 (TN): 阴性数据中被预测为阴性的数据
- 假阴性 (FN): 阳性数据中被预测为阴性的数据
常用的评估指标
- 灵敏度 (Sensitivity, Sn): 对于真实的数据,能够测成“真”的比例是多少 - (Type II error)
- 特异性 (Specificity, Sp): 对于阴性的数据,能够预测成“假”的比例是多少 - (Type I error)
- 准确性 (Accuracy, Ac): 对于整个数据集(包括阳性和阴性数据),预测总共的准确比例是多少
- 马修相关系数(Mathew correlation coefficient, MCC): 当阳性数据的数量与阴性数据的数量差别较大时,能够更为公平的反映预测能力,值域
[-1,1]
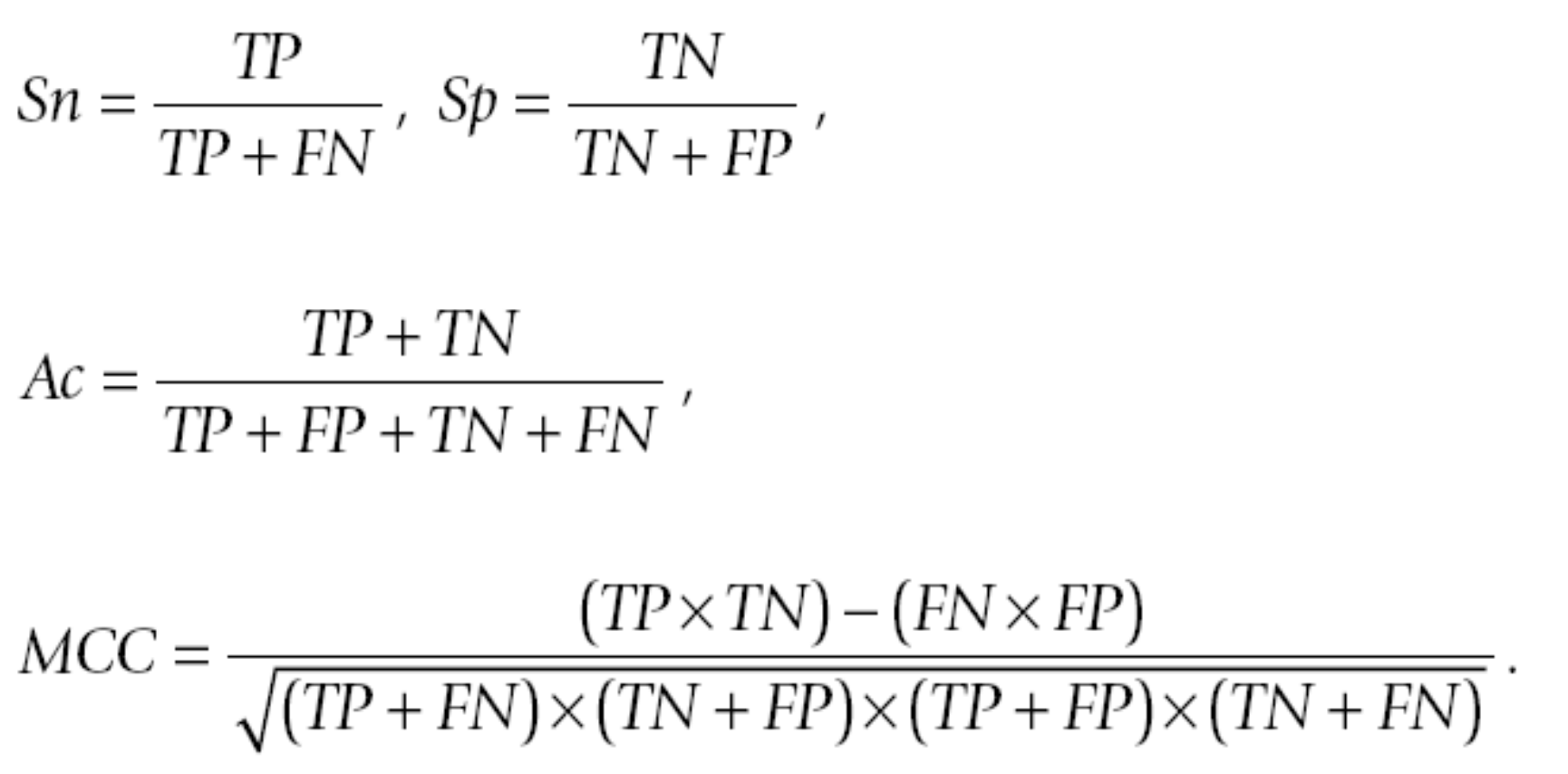
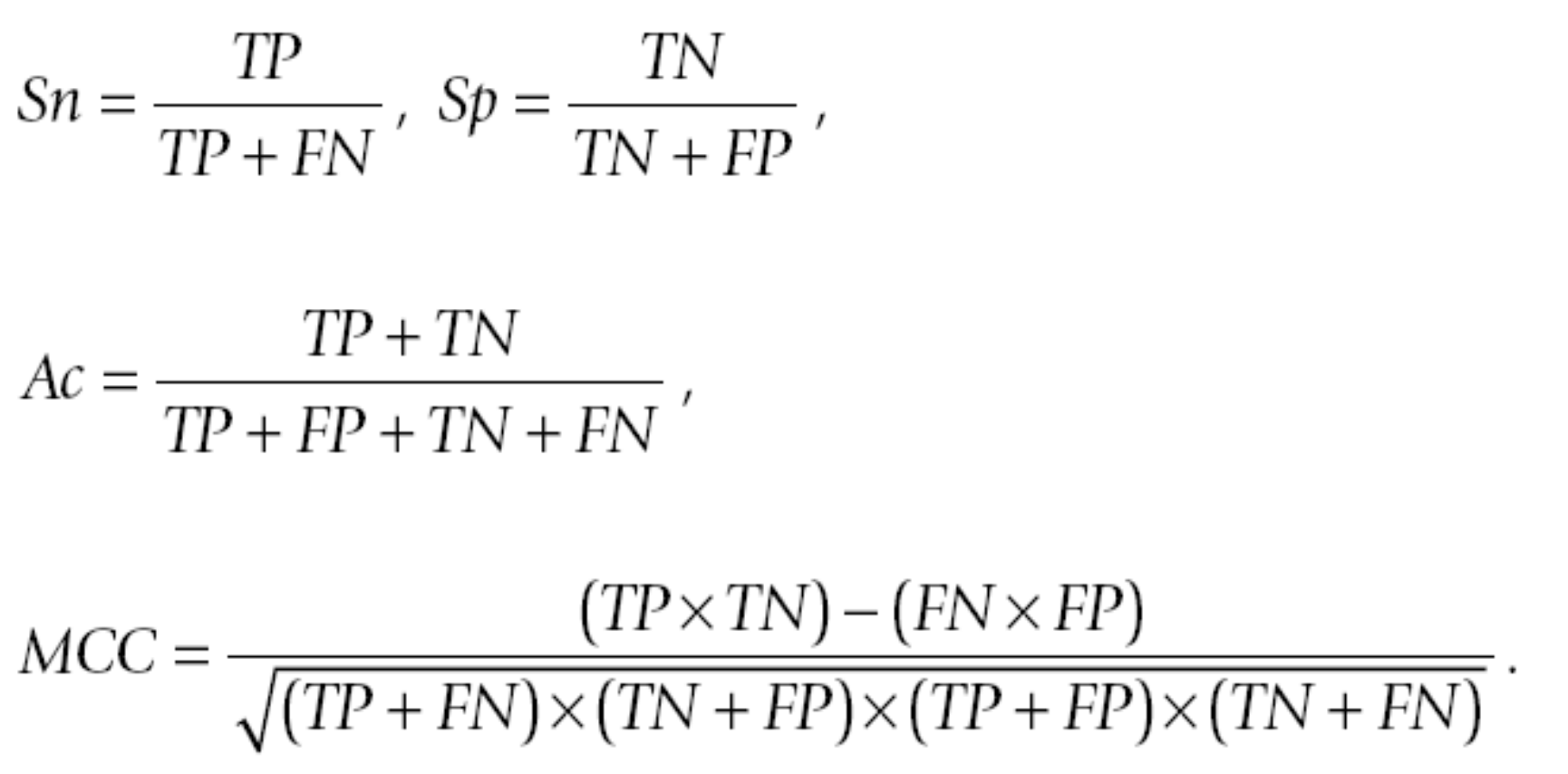
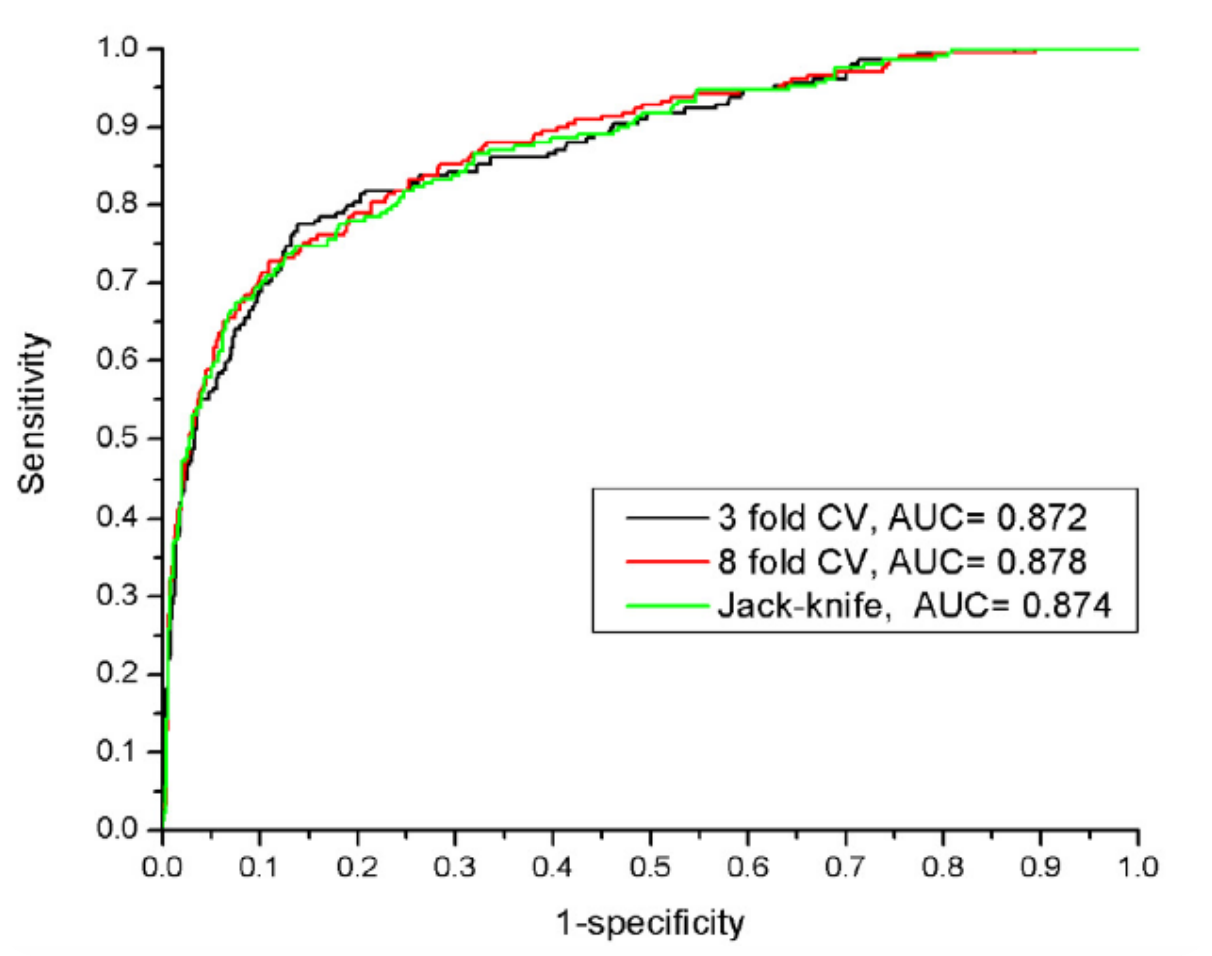
ROC curve
- X轴:1-Sp
- Y轴:Sn
- AUC(area under the curve)
- 值:ROC的面积越大,预测能力越强

预测性能的评估
自检法 (Self-consistency validation)
- 训练数据当成测试数据
- 训练数据中所有的阳性数据为测试数据中的阳性数据
- 训练数据中所有的阴性数据为测试数据中的阴性数据
- 反映当前预测工具对目前已知的数据的预测能力
- 假设:根据目前已知的数据所构建的计算模型能够反映未知的数据的模式
- 缺点:不能反映计算模型的稳定性
除一法 (Leave-one-out validation)
- 每次从数据集中去掉一个,包括阳性数据和阴性数据
- 利用剩下的数据重新训练,并构建新的计算模型
- 对去掉的这一个数据进行打分
- 保证每个数据去掉一次,从而得到所有数据的分值
- 计算各个阈值的Ac, Sn, Sp和MCC
- 计算AUC值,作为准确性的评价指标
N折交叉法 (N-fold cross-validation)
- 将数据集分成n组,并保证阳性数据与阴性数据的比例与原数据相同
- 将n-1组作为训练数据,重新训练并构建计算模型;1组不用于训练
- 将n-1组的数据重新分为n组,其中n-1组用来构建模型,1组用于调参
- 对不用训练的1组进行打分,计算性能
- 重复n次,使每组数据都用于独立测试集1次
- 选取AUC最高模型
预测性能及稳定性
- 自检法: 反映预测性能
- 留一法 & N折交叉法: 反映预测系统的稳定 性
- 预测性能 vs. 检验性能
- 差距较小:系统稳定
- 差距过大:系统不稳定,数据过训练
阈值的确定
- Threshold 或 Cut-off:
- 人为设定,主要依据经验
- 给定阈值以上或以下预测为阳性
- 即利用阈值进行“一刀切”
- 确定阈值的一般方法
- 传统策略:平衡Sn和Sp,使两者大致相当
- 实际应用:高Sp低Sn保证预测结果的可靠性
- MCC最大值,保证综合预测性能最高
- ……
过训练 (Overfitting/Overtraining)
- 根据已知数据构建的模型只能很好的适用于训练数据
- 不适合用来预测
- 对训练数据的微小改变对于预测性能影响过大
- 预测工具过训练:只能很好的符合训练数据,而对新数据则性能很差
如何评估算法的准确性?


线性模型 & 决策树
- 线性回归 (Linear Regression)
- $f(x)=ax+b$
- 对数几率回归/逻辑回归(Logistic regression)
- $f(x)=\frac{1}{1+e^{-ax-b}}$
- 信息熵
- $ Ent(D)=-\sum_{k=1}^{ \mid y \mid } D\ log_{2} {p_k}$
- 信息增益
- $ Gain(D,a) = Ent(D) - \sum_{v=1} ^ {V} \frac{ D^v \mid }{\mid D \mid}Ent(D^v)$
神经网络 & 支持向量机
- 单层 & 多层神经网络
- 误差逆传播 (Back propagation, BP)


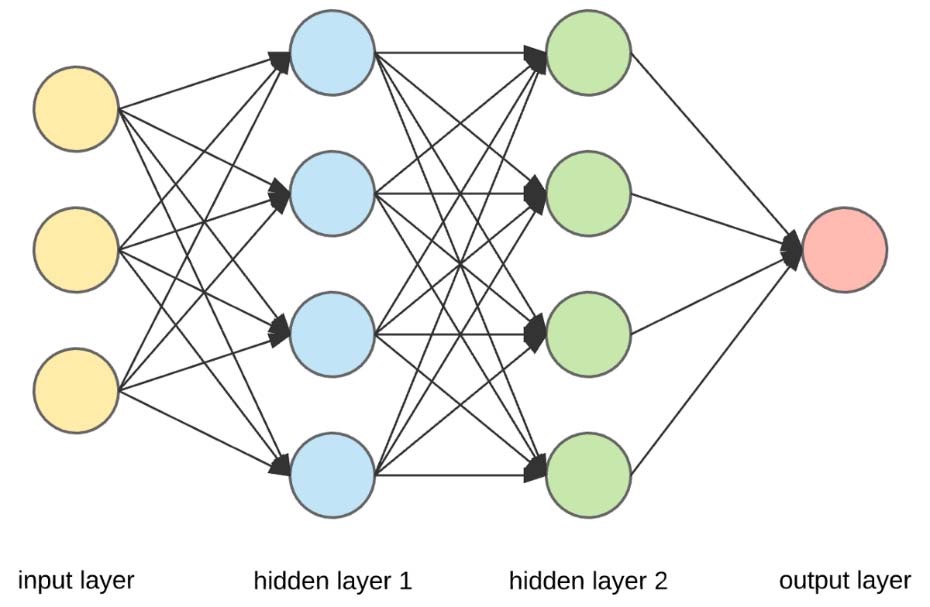

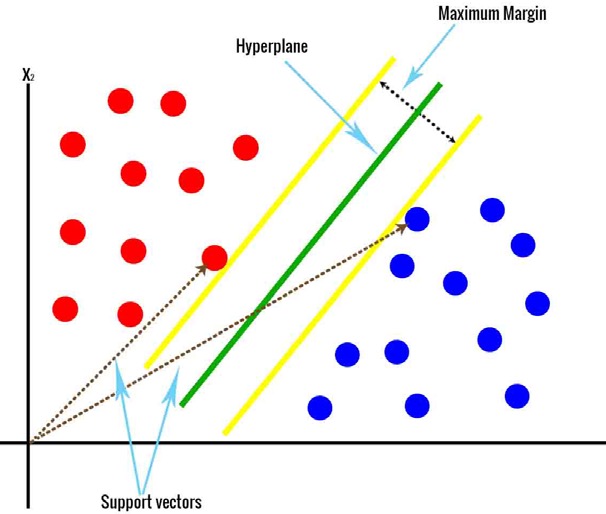
- 划分超平面
- $f(x)=w^{T}x+b$
- 核函数
- 将线性不可分样本映射到更高维空间,从而线性可分

贝叶斯分类器 & 集成学习
- 贝叶斯最优分类器
- $h^{*} = arg \max_{c \in Y}P(C\mid x)$
- $P(C\mid x) = \frac{P(x\mid C)P(C)}{P(x)}$
- 集成学习的错误率:
- $e \leq \exp { -\frac{1}{2} T \cdot {1 - 2\epsilon}^2 }$
神经元、卷积层、池化层和输出层
- 神经元激活函数
- $RELU(x)=\begin{cases} x, & \text{if } x>0 \ 0, & \text{if } x\leq 0 \end{cases}$
- 最大池化(Max pooling)
- 卷积层
- 输出
- $sigmoid(x)=\frac{1}{1+e^{-x}}$
Large Language Models
Reinforcement Learning from Human Feedback (RLHF)
- 四代语言模型的演化过程
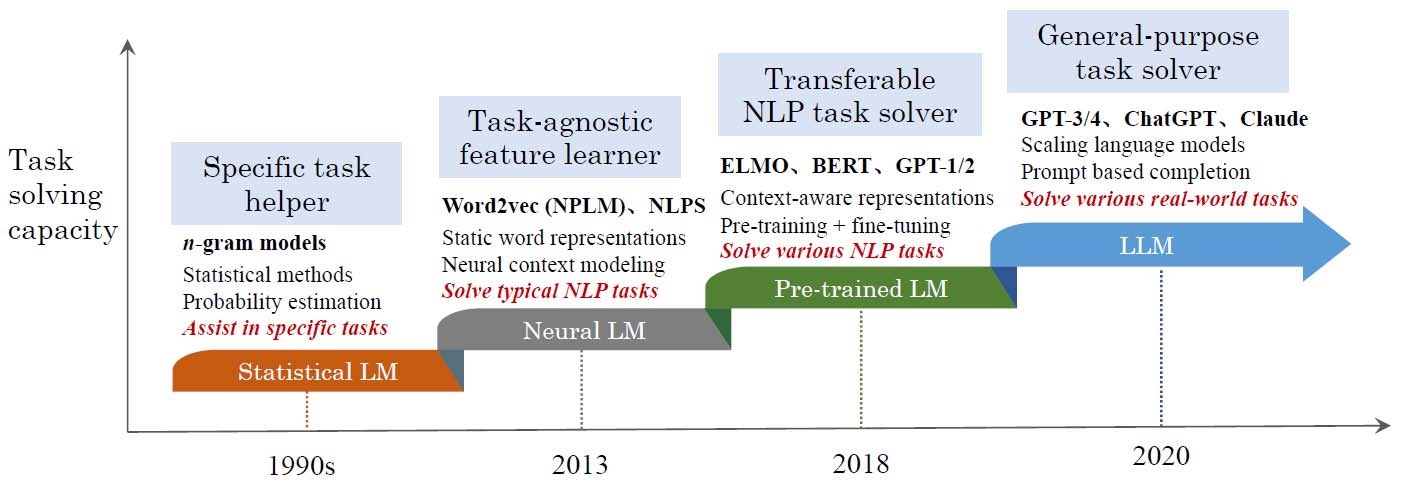

- 大型语言模型研发的时间线
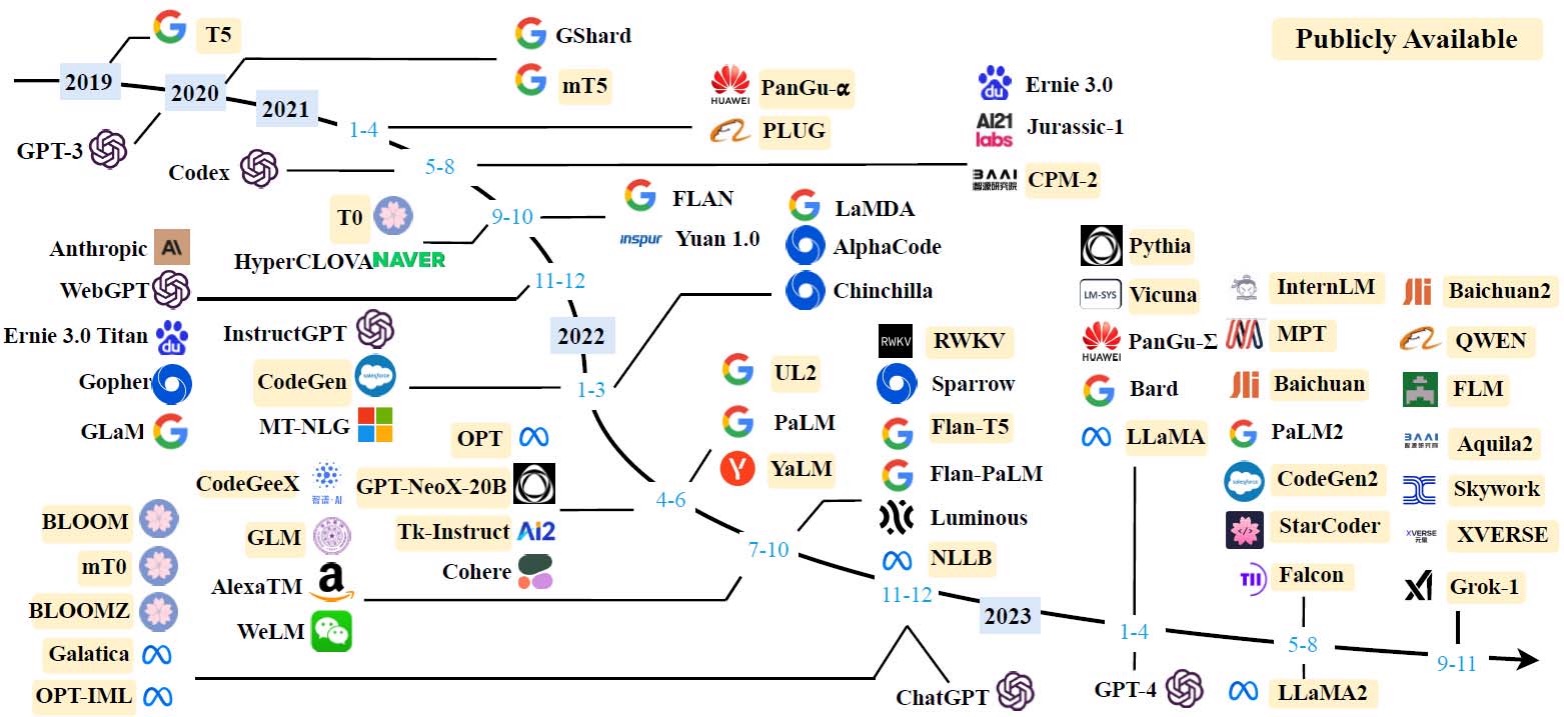

- 人类反馈的强化学习算法
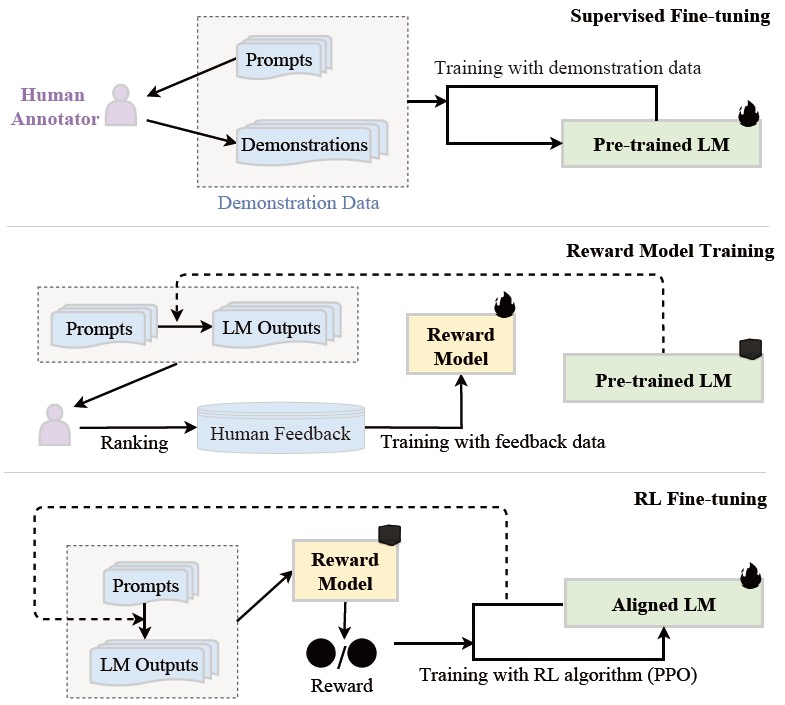

AGI and its developments
Generative adversarial network, GAN
生成对抗网络
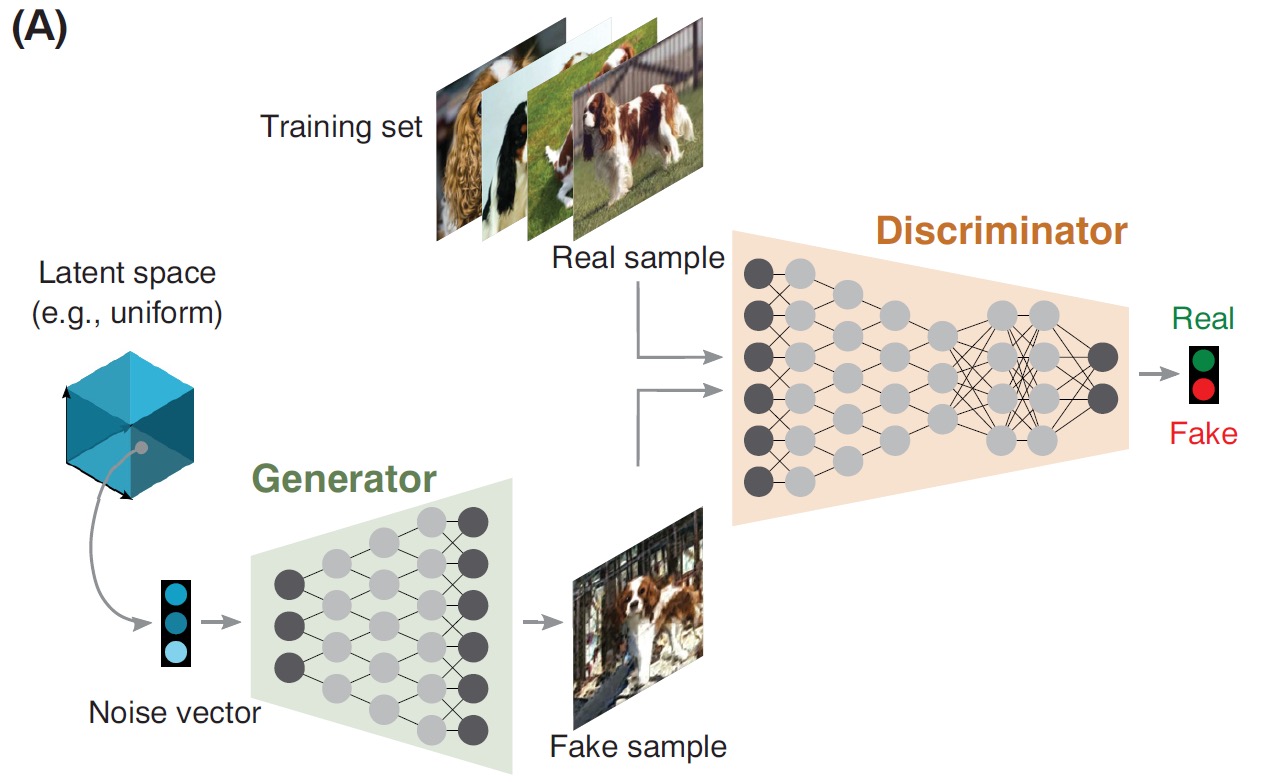

Variational Autoencoder, VAE
变分自编码器
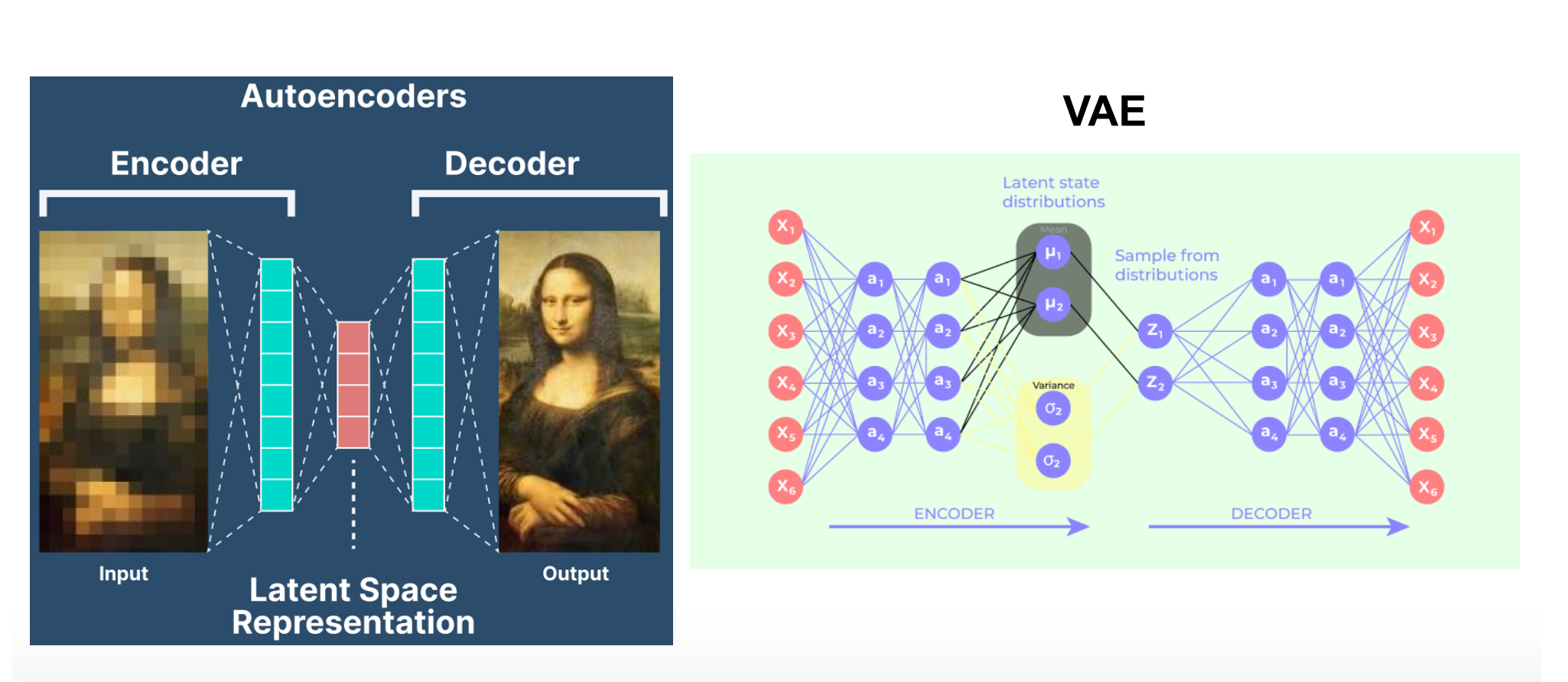

Stable Diffusion, SD
稳定扩散
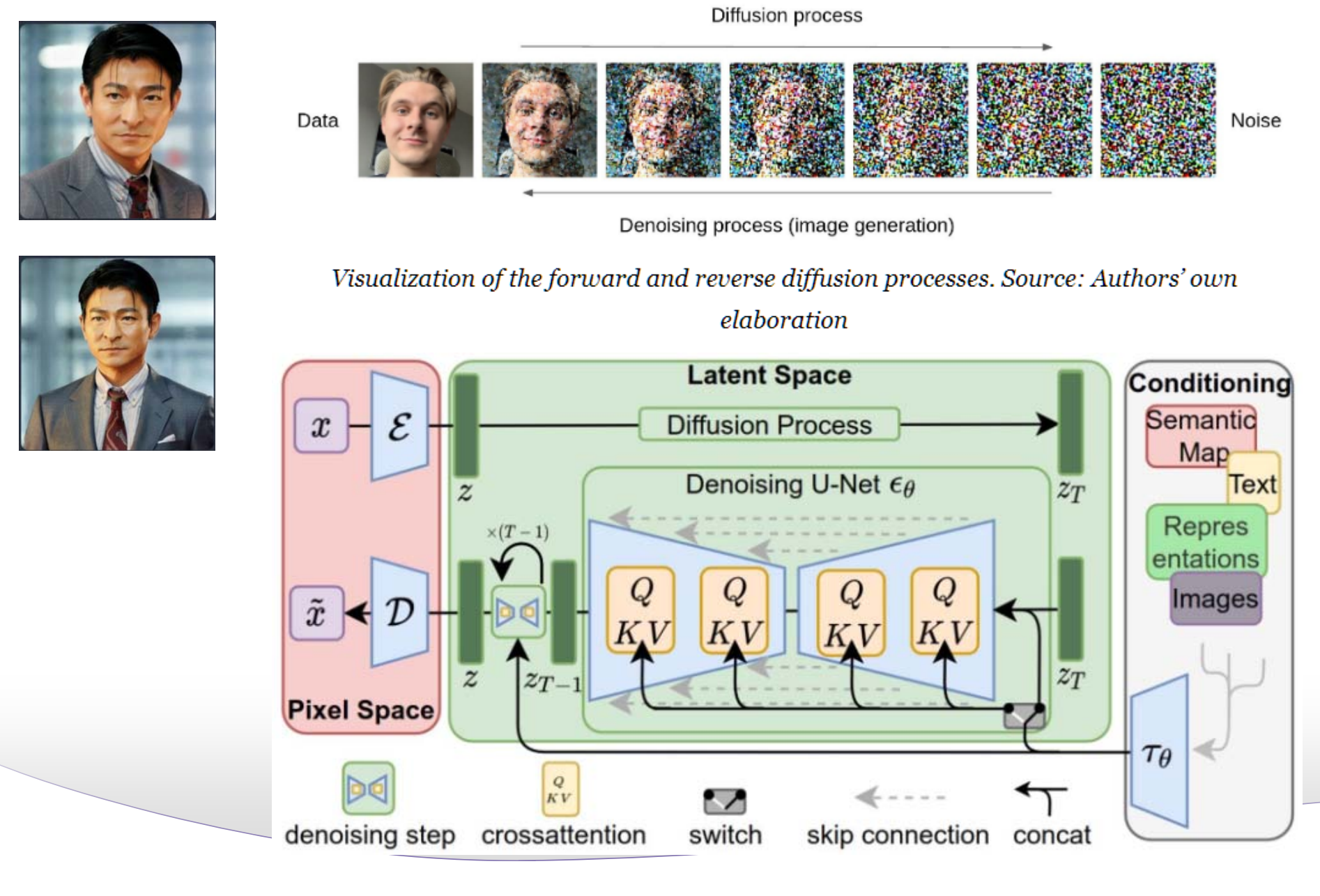

Text Encoder, TE
文本编码器
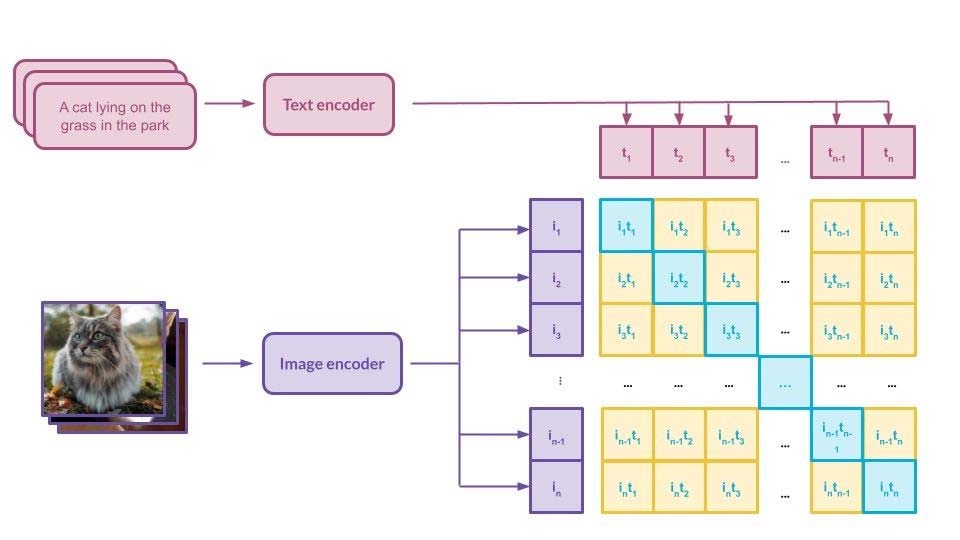

And more…
深度学习常用软件包
- Keras
Click to visit it’s Official Website.
生物序列的概率模型
概率模型
一个能够通过不同的概率产生不同结果的模型。概率模型可以模拟或者仿真某一类型的所有事件,并且对每个事件赋予一个概率。
色子模型
一个色子存在6个概率值:$p_1, p_2, …, p_6$,其中掷出i的概率为$p_i (i=1, 2, …, 6)$。因此:
$p_i \geq 0, \sum_{i=1}^{6} p_i = 1$
考虑三次连续的掷色子,结果为 $[1,6,3]$,则总概率为:$p_1 \cdot p_6 \cdot p_3$
二项分布
- 二项分布是n次独立的伯努利试验的和
- 伯努利试验:只有两种结果的随机试验
- 二项分布的概率质量函数:
- $P(X=k) = C_n^k p^k (1-p)^{n-k}$
- $C_n^k = \frac{n!}{k!(n-k)!}$
- 二项分布的期望值:$E(X) = np$
- 二项分布的方差:$Var(X) = np(1-p)$
e.g. 一枚硬币掷10次,正面朝上的次数为$X$,硬币正面朝上的概率为$p=0.5$,则$X$服从二项分布$B(10, 0.5)$,有$k$次正面朝上的概率为:$P(X=k) = C_{10}^k 0.5^k 0.5^{10-k}$。
酵母的全基因组复制
See the original article at this link.
DOI: 10.1038/nature02424
泊松分布
稀有事件发生的概率:在一个连续的时间或空间中,稀有离散变量出现的概率
$P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}$
- $\lambda$:事件发生的平均次数
- $k$:事件发生的次数
泊松分布的均值和方差都是$\lambda$。
细菌 vs. 噬菌体
细菌对噬菌体的应答
- 数十亿细菌与噬菌体混合后,几乎所有的细菌将被杀死
- 仅有很少的细菌能够存活,生长成克隆,并且对噬菌体具有特异性抵抗能力
- 进化:细菌是否有基因?受到噬菌体攻击如何生存?
- 拉马克机制:获得性遗传免疫 假说 细菌在接触到噬菌体后,小概率产生抵抗,不需要基因或遗传物质
- 孟德尔机制:突变假说 细菌在接触到噬菌体后,产生突变,产生抵抗,需要基因或遗传物质
细菌生存的潜在机制
- 孟德尔 – 遗传变异
- 细菌在噬菌体攻击之前已经具有抵抗能力,不需要与病毒相互作用,受到攻击时也不产生新的突变
- 具有抵抗能力的细菌随时间比例增加
- 非泊松分布:抵抗性细菌由紧密相关的个体构成群落
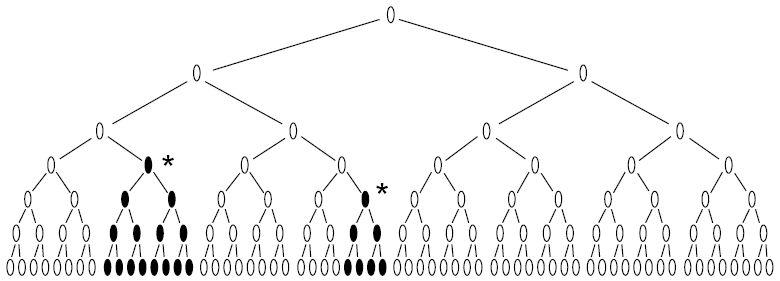

- 拉马克 – 获得性遗传
- 细菌在受到攻击的时候才产生免疫能力
- 具有抵抗能力的细菌在受到攻击时的比例恒定
- 泊松分布:每一个抵抗是一个独立的事件


结果:方差分析
泊松分布的方差等于均值,而非泊松分布的方差大于均值
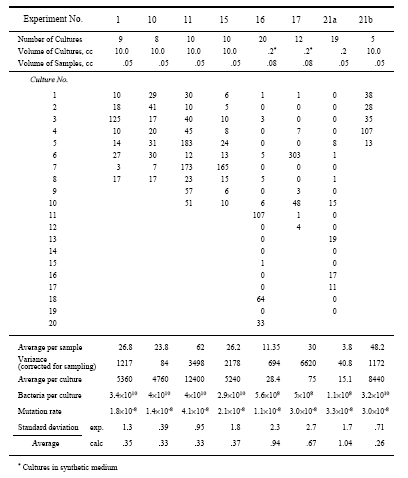

结论:细菌的抵抗性是由基因决定的,而非获得性遗传。
例:鸟枪法的覆盖率
Lander-Waterman Model
假设:需要测序的BAC长度200 kbp
- 测序深度:10x
- 测序长度:500 bp
- 总共测序的序列数量:N
- 总覆盖率 $C=Np$(每个点平均覆盖到的次数)
$N = \frac{200000 \times 10}{500} = 4000$
点X被覆盖k次的概率:二项分布~泊松分布
$P(X=k) = C_n^k p^k (1-p)^{n-k} \approx \frac{C^k e^{-C}}{k!}$
当点X一次都不被覆盖时,$k=0$; 此时的概率为:$P(X=0) = e^{-C}$。
超几何分布
一种不放回抽样的概率分布
- 从有限个物件中抽出$n$个物件,其中包含$m$个特定种类的物件的概率分布
- 超几何分布的概率质量函数:
- $P(X=k) = \frac{C_M^k C_{N-M}^{n-k}}{C_N^n}$
- $E(X) = n \frac{M}{N}$
- $Var(X) = n \frac{M}{N} \frac{N-M}{N} \frac{N-n}{N-1}$
e.g. 从一副52张的扑克牌中抽取5张,其中有2张黑桃的概率是多少?
- $N=52, M=13, n=5, k=2$
- $P(X=2) = \frac{C_{13}^2 C_{39}^3}{C_{52}^5}$
- $E(X) = 5 \frac{13}{52}$
- $Var(X) = 5 \frac{13}{52} \frac{39}{52} \frac{47}{51}$
- $P(X=2) = 0.4115$
e.g. 有N个球,其中红球M个,白球N-M个,每次拿出一个球不放回,总共n次,其中有至少有m个球是红球的概率为多少?
- $P(X \geq m) = 1 - P(X < m-1)$
- $P(X < m-1) = \sum_{k=0}^{m-1} \frac{C_M^k C_{N-M}^{n-k}}{C_N^n}$
例:基因组中的SNP
- 人类基因组中的SNP(单核苷酸多态性)的分布
- 人类基因组中的SNP的分布是超几何分布
研究者从26873个人类蛋白质中预测了2264个具有某种特定功能的底物,并进行进一步的分析。其中,有421个人类蛋白质具有某种功能结构域D,而在预测的2264个底物中,有94个蛋白质具有结构域D
问:结构域D在2264个底物中是显著出现,显著不出现,还是随机出现?
- $N=26873, M=421, n=2264, k=94$
- $P(X=94) = \frac{C_{421}^{94} C_{26452}^{2170}}{C_{26873}^{2264}}$
- $P(X=94) = 0.0001$
- $\dfrac{ \dfrac{m}{n} }{ \dfrac{M}{N} } = 2.65$
因此,问题转化:在26873个人的蛋白质中,抓出2264个蛋白质,其中至少有94个蛋白质具有功能结构域的概率是多少?
$p-value = P(m\slash \geq m) = 1 - P(m\slash < m-1) = 1 - \sum_{k=0}^{m-1} \frac{C_M^k C_{N-M}^{n-k}}{C_N^n}$
统计显著性
- 考虑两个假设$H_0$(空假设)和$H_1$(备择假设)
- H0代表随机情况下事件出现的概率
- H1代表当前出现事件的概率
- 如果$H_0 << H_1$,则拒绝$H_0$,接受$H_1$
- 统计显著:$H_0$被拒绝,接受$H_1$
- 超几何分布的$p-value$u
- “完全随机状态下”事件出现的概率,即p-value=H0
- H1=1
随机序列模型
- 随机序列模型:描述序列的生成过程
- 假设一个残基$a$随机出现的概率为$q_a$,并且该概率独立于其它残基而存在,则序列$S$的概率为:
- $P(S) = \prod_{i=1}^{L} q_{S_i}$
- $L$:序列的长度
- $S_i$:序列中的第$i$个残基
- $q_{S_i}$:残基$S_i$出现的概率
条件、连接、边际的概率
- 考虑两个骰子,$X$和$Y$,$X$的概率分布为$p(x)$,$Y$的概率分布为$p(y)$
- 条件概率:用骰子$X$的结果来预测骰子$Y$的结果
- $p(y\mid x) = \frac{p(x,y)}{p(x)}$
- 连接概率:两个骰子同时出现的概率
- $p(x,y) = p(x)p(y)$
- 边际概率:单个骰子的概率
- $p(x) = \sum_{y} p(x,y)$